On the Anatomy of MCMC-Based Maximum Likelihood Learning of Energy-Based Models

Erik Nijkamp^*, Mitch Hill^*, Tian Han, Song-Chun Zhu, Ying Nian Wu

^* Equal contributions
University of California, Los Angeles (UCLA), USA

Abstract

This study investigates the effects of Markov chain Monte Carlo (MCMC) sampling in unsupervised Maximum Likelihood (ML) learning. Our attention is restricted to the family of unnormalized probability densities for which the negative log density (or energy function) is a ConvNet. We find that many of the techniques used to stabilize training in previous studies are not necessary. ML learning with a ConvNet potential requires only a few hyper-parameters and no regularization. Using this minimal framework, we identify a variety of ML learning outcomes that depend solely on the implementation of MCMC sampling. On one hand, we show that it is easy to train an energy-based model which can sample realistic images with short-run Langevin. ML can be effective and stable even when MCMC samples have much higher energy than true steady-state samples throughout training. Based on this insight, we introduce an ML method with purely noise-initialized MCMC, high-quality short-run synthesis, and the same budget as ML with informative MCMC initialization such as CD or PCD. Unlike previous models, our energy model can obtain realistic high-diversity samples from a noise signal after training. On the other hand, ConvNet potentials learned with non-convergent MCMC do not have a valid steady-state and cannot be considered approximate unnormalized densities of the training data because long-run MCMC samples differ greatly from observed images. We show that it is much harder to train a ConvNet potential to learn a steady-state over realistic images. To our knowledge, long-run MCMC samples of all previous models lose the realism of short-run samples. With correct tuning of Langevin noise, we train the first ConvNet potentials for which long-run and steady-state MCMC samples are realistic images.

Paper

The publication can be obtained here.

@article{nijkamphill2019anatomy,
  title={On the Anatomy of MCMC-Based Maximum Likelihood Learning of Energy-Based Models},
  author={Nijkamp, Erik and Hill, Mitch and Han, Tian and Zhu, Song-Chun and Wu, Ying Nian},
  journal={AAAI},
  year={2020}
}

Poster

The poster can be obtained here.

Code

The code can be obtained here.

Diagnosing MCMC-Based Maximum Likelihood

This work is motivated by the observation that all prior works that learn energy-based models with a ConvNet potential exhibit unrealistic long-run MCMC samples, as shown in Figure 1. The oversaturated appearance of long-run MCMC samples leads to two important conclusions: 1) prior ConvNet potentials do not assign probability mass in realistic regions of the image space, and 2) short-run synthesis is successful even though MCMC sampling with informative initialization such as CD and PCD is highly non-convergent.

Figure 1: Prior works that learn unnormalized densities with ConvNet potentials exhibit oversaturated long-run MCMC samples, indicating that the learned density is not valid. Left: Xie et al., 2016, Middle: Lee et al., 2017, Right: Du and Mordatch, 2019.

Analysis of the MCMC-based ML learning process reveals two axes which govern each update of the model parameters. These axes are 1) the energy difference between data samples and MCMC samples (a negative difference indicates that data samples are more likely than MCMC samples, and a positive difference indicates the opposite) and 2) the convergence of MCMC samples with respect to the current model steady-state. All stable learning outcomes exhibit oscillation along the first axis, meaning that data samples and MCMC samples frequently exchange the role being more likely or less likely. All prior implementations fall exclusively on the non-convergent side of the second axis throughout training, despite the fact that informative initialization methods such as PCD are used with the justification that these methods facilitate convergence. Our main experimental contributions are: 1) the first non-convergent learning method with purely noise-initialized MCMC, and 2) the first convergent ConvNet potentials with realistic long-run MCMC samples. Our diagnosis and contributions are summarized in Figure 2.

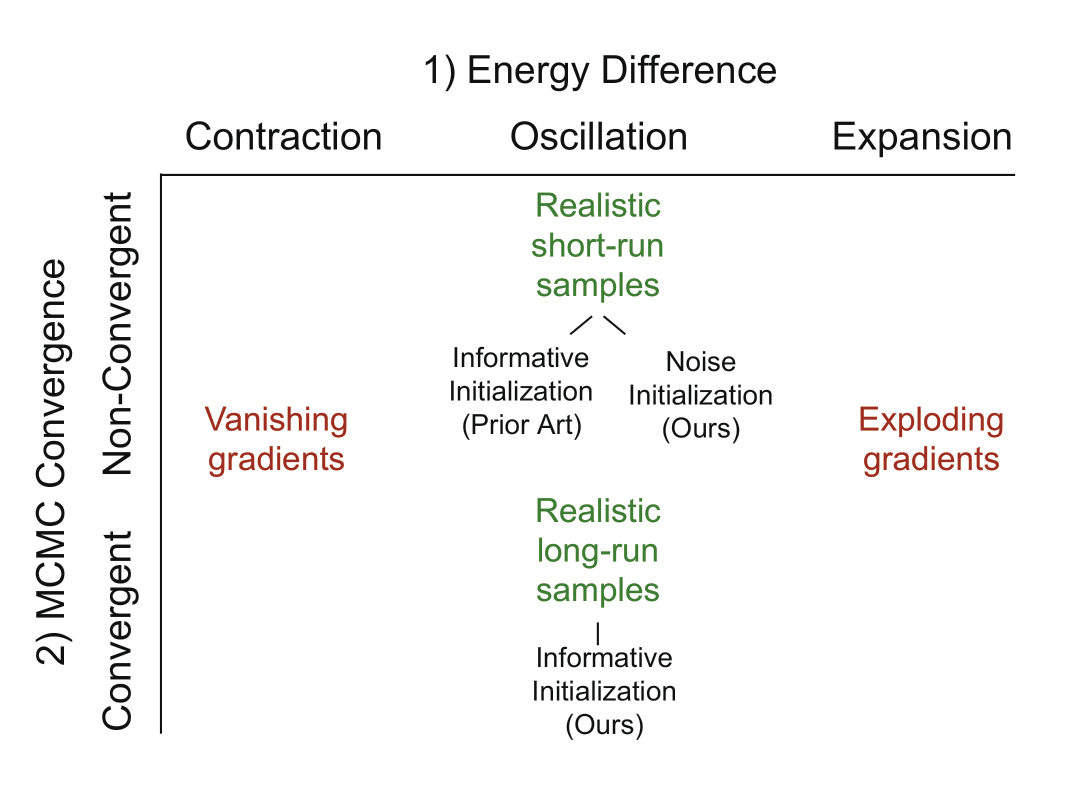
Figure 2: Two axes that govern each update of MCMC-based ML learning, and our contributions along the axes.

Experiments

Experiment 1: Learning Outcomes for 2D Toy Data

We illustrate the distinction between convergent and non-convergent outcomes for 2D densities in Figure 3. The short-run MCMC densities used in training (obtained via kernel density estimation) closely match the ground truth for both convergent and non-convergent outcomes. However, the actual energy function learned by the non-convergent model is sharply concentrated and inaccurrate, while the energy function from convergent learning closely matches the ground truth.

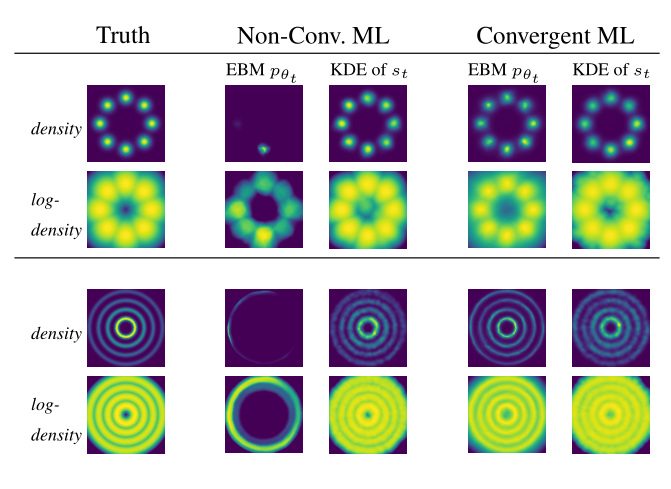
Figure 3: Illustration of non-convergent and convergent learning outcomes for 2D toy data.

Experiment 2: Learning Outcomes for Image Data

The same distinction between non-convergent and convergent learning can be observed for energy functions of high-dimensional image data, as shown in Figure 4. The short-run MCMC samples of both non-convergent and convergent models closely resemble the training data. However, long-run MCMC samples of the non-convergent model are oversaturated, while long-run samples of a convergent model are realistic and similar to short-run samples. Convergent results from two different kinds of networks are presented.

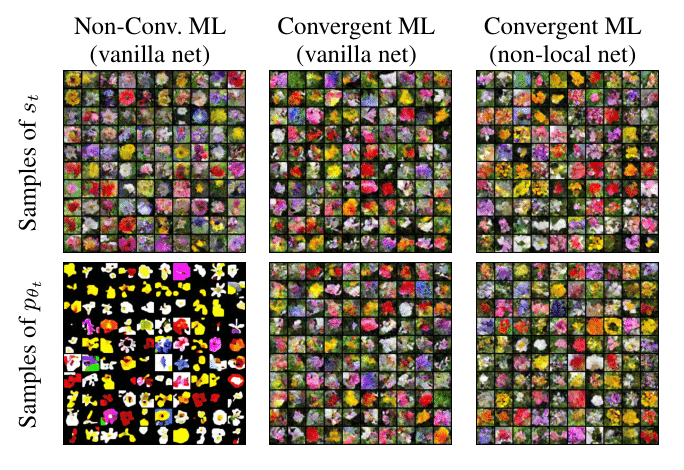
Figure 4: Illustration of non-convergent and convergent learning outcomes for the Oxford Flowers 102 dataset.

Experiment 3: Non-Convergent Learning with Noise-Initialized MCMC

We show that informative initialization of MCMC samples (i.e. use of methods such as CD and PCD) is not essential for stable and efficient non-convergent learning. We implement ML learning with purely noise-initialized MCMC throughout training to learn a non-invertible flow capable of generating realistic images from a latent noise signal. Unlike models trained with persistent chains, models trained with purely noise-initialized MCMC can easily generated new samples after learning has concluded. Results for the Oxford Flowers 102 dataset are shown in Figure 5. See our companion paper Nijkamp et al., 2019 for a thorough investigation of non-convergent noise-initialized learning.

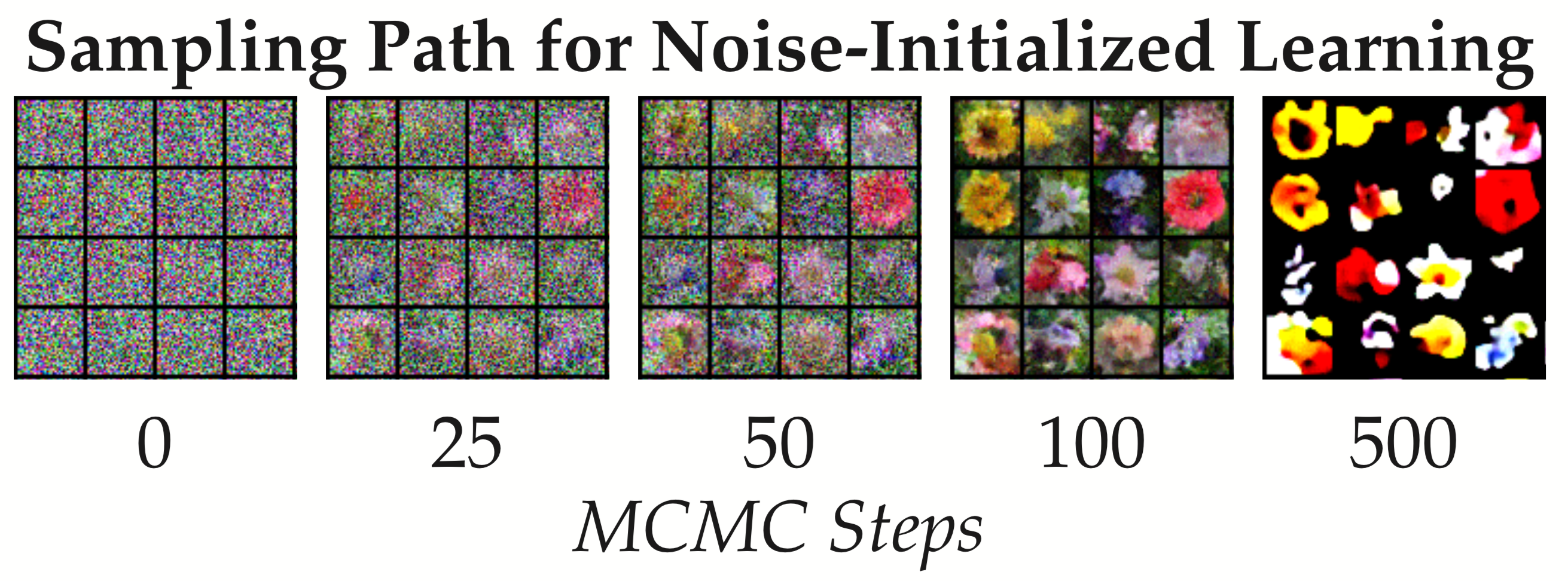
Figure 5: Generation of images using 100 MCMC steps from uniform noise with a non-convergent model trained using purely noise-initialized MCMC.

Experiment 4: Mapping the Energy Landscape of a Convergent Energy

The metastable structures of convergent energy functions correspond to image concepts that are recognizable to humans. We apply the method used in Hill et al., 2018 to map the macroscopic non-convex structures of a convergent energy trained on the Oxford Flowers 102 dataset. The large-scale energy basins represent meaningful clusters among flower images, as shown in Figure 6.

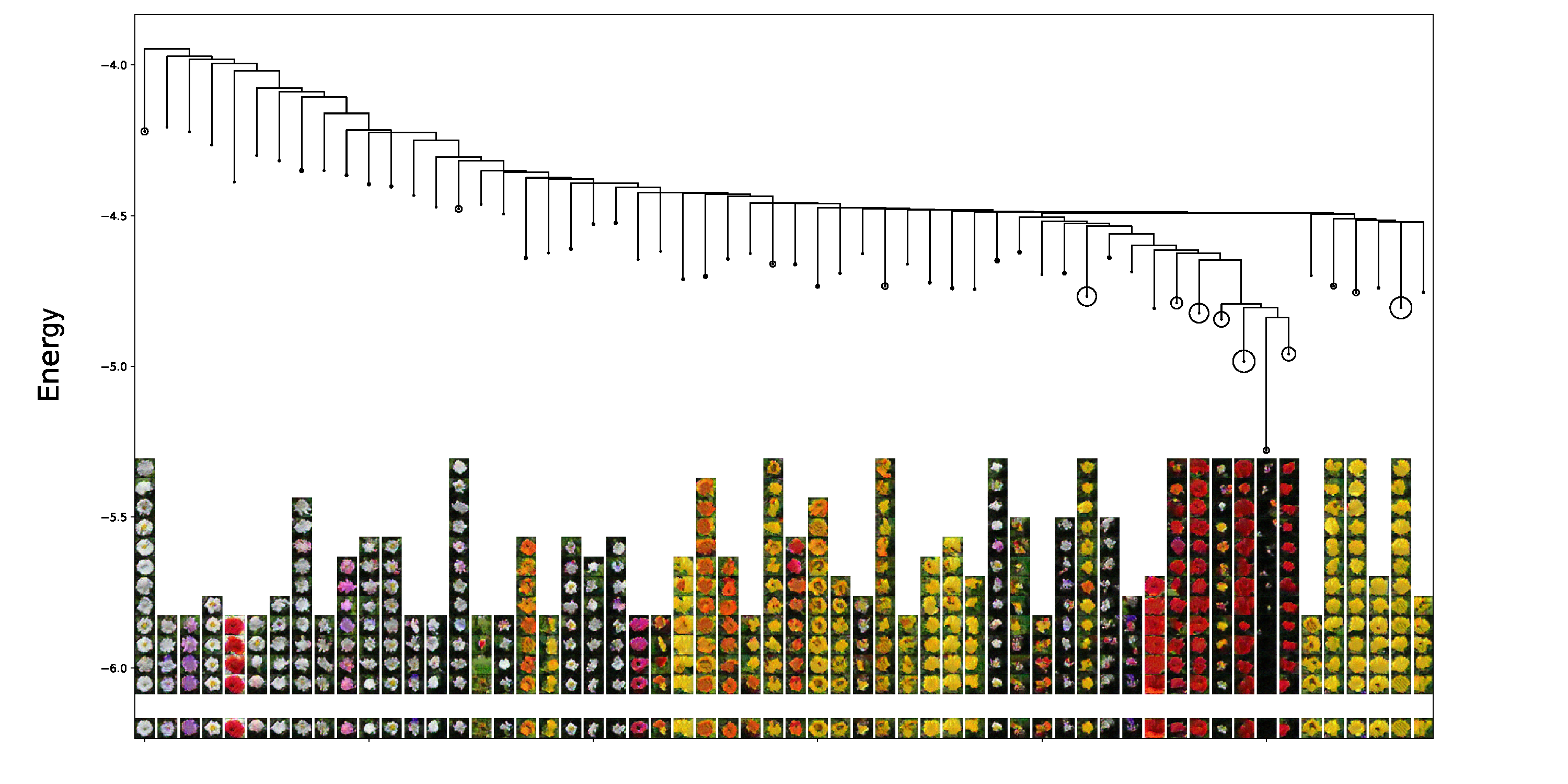
Figure 6: Metastable structures of a convergent energy function trained on the Oxford Flowers 102 dataset.

Acknowledgements

The work is supported by DARPA XAI project N66001-17-2-4029; ARO project W911NF1810296; and ONR MURI project N00014-16-1-2007; and XSEDE grant ASC170063. We thank Prafulla Dhariwal and Anirudh Goyal for helpful discussions.