Learning Multi-layer Latent Variable Model via Variational Optimization of Short Run MCMC for Approximate Inference
University of California, Los Angeles (UCLA), USA
Stevens Institute of Technology, USA
Abstract
This paper studies the fundamental problem of learning deep generative models that consist of multiple layers of latent variables organized in top-down architectures. Such models have high expressivity and allow for learning hierarchical representations. Learning such a generative model requires inferring the latent variables for each training example based on the posterior distribution of these latent variables. The inference typically requires Markov chain Monte Caro (MCMC) that can be time consuming. In this paper, we propose to use noise initialized non-persistent short run MCMC, such as finite step Langevin dynamics initialized from the prior distribution of the latent variables, as an approximate inference engine, where the step size of the Langevin dynamics is variationally optimized by minimizing the Kullback-Leibler divergence between the distribution produced by the short run MCMC and the posterior distribution. Our experiments show that the proposed method outperforms variational auto-encoder (VAE) in terms of reconstruction error and synthesis quality. The advantage of the proposed method is that it is simple and automatic without the need to design an inference model.
Paper
The publication can be obtained here.
@article{nijkamp2020inf,
title={Learning Multi-layer Latent Variable Model via Variational Optimization of Short Run MCMC for Approximate Inference},
author={Nijkamp, Erik and Pang, Bo and Han, Tian and Zhu, Song-Chun and Wu, Ying Nian},
journal={ECCV},
year={2020}
}
Contributions
(1) We propose short run MCMC for approximate inference of latent variables in deep generative models.
(2) We provide a method to determine the optimal step size, or in general, hyper-parameters of the short run MCMC.
(3) We demonstrate learning of multi-layer latent variable models with high quality samples and reconstructions.
Code
The code can be obtained here.
Experiments
Experiment 1: Synthesis
We contrast the synthesis of a generator model \(g_\theta(z)\) with \(L=5\) latent layers learned by Ladder-VAE and our proposed short run MCMC infernece method in Figure 1. Despite its simplicity, short run MCMC is competitive with elaborate means of inference in VAE models and flow-based models, such as Glow.


Figure 1: Generated samples for top-down models \(g_\theta(z)\) learned by Ladder-VAE (left) and our proposed means of approximate inference by short run MCMC (right) on CelebA \((64 \times 64)\).
Experiment 2: Reconstruction
We evaluate the accuracy of the learned short run MCMC inference dynamics \(q_{s, \theta_t}(z|x_i)\) by reconstructing test images. In contrast to traditional MCMC posterior sampling with persistent chains, short run inference with small \(K\) allows not only for efficient learning on training examples, but also the same dynamics can be recruited for testing examples. Figure 2 compares the reconstructions of learned generators with \(L=5\) layers by Ladder-VAE and short run inference on CelebA \((64\times64\times3)\). The fidelity of reconstructions by short run MCMC inference appears qualitatively improved over VAE

Figure 2: Comparison of reconstructions between Ladder-VAE samples and our method on CelebA \((64\times64\times3)\) with \(L=5\). Top: original test images. Middle: reconstructions from VAE. Bottom: reconstructions by short run inference.
Experiment 3: Inpainting
Our method can "inpaint" occluded image regions. To recover the occluded pixels, the only required modification involves the computation of \(\|x - g_\theta(z)\|^2/\sigma^2\). For a fully observed image, the term is computed by the summation over all pixels. For partially observed images, we only compute the summation over the observed pixels. Figure 3 depicts test images taken from the CelebA dataset for which a mask randomly occludes pixels in various patterns.

Figure 3: Inpainting on CelebA \((64\times64\times3)\) with \(L=5\) for varying occlusion masks. Top: original test images. Middle: occluded images. Bottom: inpainted test images by short run MCMC inference.
Experiment 4: Hierarchical representation
Multi-layer latent variable models not only demonstrate improved expressiveness over single-layer ones but also allow for learning the hierarchical structure. It can be argued that an alternative parameterization of the multi-layer generator promotes disentangled hierarchical features. We train a three-layer model with this parameterization using short run inference on SVHN. As shown in Figure 4, the three-layer latent variables capture disentangled representations, which are background color, digit identity, general structure from bottom to top layer.



Figure 4: Generated samples from a three-layer generator where each sub-figure corresponds to samples drawn when fixing the latent variables \(z\) of all layers except for one. (left) The bottom layer represents background color. (center) The second layer represents digit identity. (right) The top layer represents general structure.
Experiment 5: Variational optimization of step size
The step size \(s\) of short run MCMC may be optimized such that \(q_s(z)\) best approximates the posterior \(p_\theta(z|x)\). That is, we can optimize the step size \(s\) by minimizing \(KL(q_s(z) \| p_\theta(z|x))\) via a grid search or gradient descent. Then, we evaluate the eigenvalues of \(d F(z_0, \epsilon)/d z_0\). As both steps are computed in a differentiable manner, we may compute the gradient with respect to \(s\). Figure 5 depict the optimal step size \(s\) over learning iterations \(t\) determined by grid-search and gradient descent.
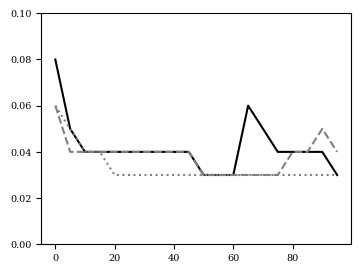
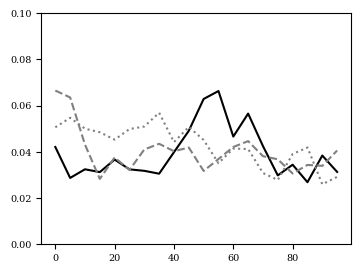
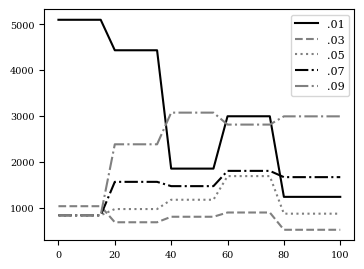
Figure 5: (left) and (center) step size \(s\) over epochs \(T\) for three individual runs with varying random seed. (right) \(E_{q_s(z)}[\log q_s(z) -\log p_\theta(x, z)]\) for step sizes \(s\) over epochs \(T\).
Acknowledgements
The work is supported by NSF DMS-2015577, DARPA XAI N66001-17-2-4029, ARO W911NF1810296, ONR MURI N00014-16-1-2007, and XSEDE grant ASC170063. We thank NVIDIA for the donation of Titan V GPUs. We thank Eric Fischer for the assistance with experiments.